Numero e
La constante matemática 
, es uno de los más importantes números reales.1 Se relaciona con muchos interesantes resultados. Por ejemplo, la derivada de la función exponencial 
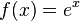, es esa misma función. El logaritmo en base e\, se llama logaritmo natural o neperiano.
El número e\,, conocido a veces como número de Euler o constante de Napier, fue reconocido y utilizado por primera vez por el matemático escocés John Napier, quien introdujo el concepto de logaritmo en el cálculo matemático.
Es considerado el número por excelencia del cálculo, así como \pi\, lo es de la geometría y el número i\, del análisis complejo. El simple hecho de que la función e^x\, coincida con su derivada hace que la función exponencial se encuentre frecuentemente en el resultado de ecuaciones diferenciales sencillas. Como consecuencia de esto, describe el comportamiento de acontecimientos físicos regidos por leyes sencillas, como pueden ser la velocidad de vaciado de un depósito de agua, el giro de una veleta frente a una ráfaga de viento, el movimiento del sistema de amortiguación de un automóvil o el cimbreo de un edificio metálico en caso de terremoto. De la misma manera, aparece en muchos otros campos de la ciencia y la técnica, describiendo fenómenos eléctricos y electrónicos (descarga de un condensador, amplificación de corrientes en transistores BJT, etc.), biológicos (crecimiento de células, etc.), químicos (concentración de iones, periodos de semidesintegración, etc.), y muchos más.
El número e\,, al igual que el número \pi\, y el número áureo (φ), es un irracional, no expresable por la razón de dos enteros; o bien, no puede ser expresado con un número finito de cifras decimales o con decimales periódicos. Además, es un número trascendente, es decir, que no puede ser obtenido mediante la resolución de una ecuación algebraica con coeficientes racionales.
Su valor aproximado (truncado) es:e, ≈ 2,71828 18284 59045 23536 02874 71352 66249 77572 47093 69995...
, es uno de los más importantes números reales.1 Se relaciona con muchos interesantes resultados. Por ejemplo, la derivada de la función exponencial 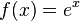, es esa misma función. El logaritmo en base e\, se llama logaritmo natural o neperiano.El número e\,, conocido a veces como número de Euler o constante de Napier, fue reconocido y utilizado por primera vez por el matemático escocés John Napier, quien introdujo el concepto de logaritmo en el cálculo matemático.
Es considerado el número por excelencia del cálculo, así como \pi\, lo es de la geometría y el número i\, del análisis complejo. El simple hecho de que la función e^x\, coincida con su derivada hace que la función exponencial se encuentre frecuentemente en el resultado de ecuaciones diferenciales sencillas. Como consecuencia de esto, describe el comportamiento de acontecimientos físicos regidos por leyes sencillas, como pueden ser la velocidad de vaciado de un depósito de agua, el giro de una veleta frente a una ráfaga de viento, el movimiento del sistema de amortiguación de un automóvil o el cimbreo de un edificio metálico en caso de terremoto. De la misma manera, aparece en muchos otros campos de la ciencia y la técnica, describiendo fenómenos eléctricos y electrónicos (descarga de un condensador, amplificación de corrientes en transistores BJT, etc.), biológicos (crecimiento de células, etc.), químicos (concentración de iones, periodos de semidesintegración, etc.), y muchos más.
El número e\,, al igual que el número \pi\, y el número áureo (φ), es un irracional, no expresable por la razón de dos enteros; o bien, no puede ser expresado con un número finito de cifras decimales o con decimales periódicos. Además, es un número trascendente, es decir, que no puede ser obtenido mediante la resolución de una ecuación algebraica con coeficientes racionales.
Su valor aproximado (truncado) es:e, ≈ 2,71828 18284 59045 23536 02874 71352 66249 77572 47093 69995...
Historia
Leonhard Euler popularizó el uso de la letra e para representar la constante; además fue el descubridor de numerosas propiedades referentes a ella.
Las primeras referencias a la constante fueron publicadas en 1618 en la tabla en un apéndice de un trabajo sobre logaritmos de John Napier.2 No obstante, esta tabla no contenía el valor de la constante, sino que era simplemente una lista de logaritmos naturales calculados a partir de ésta. Se cree que la tabla fue escrita por William Oughtred.
El "descubrimiento" de la constante está acreditado a Jacob Bernoulli, quien estudió un problema particular del llamado interés compuesto. Si se invierte una Unidad Monetaria (que abreviaremos en lo sucesivo como UM) con un interés del 100% anual y se pagan los intereses una vez al año, se obtendrán 2 UM. Si se pagan los intereses 2 veces al año, dividiendo el interés entre 2, la cantidad obtenida es 1 UM multiplicado por 1,5 dos veces, es decir 1 UM x 1,502 = 2,25 UM. Si dividimos el año en 4 períodos (trimestres), al igual que la tasa de interés, se obtienen 1 UM x 1,254 = 2,4414... En caso de pagos mensuales el monto asciende a 1 UM x (1+\textstyle{1 \over 12})^{12} = 2,61303...UM. Por tanto, cada vez que se aumenta la cantidad de períodos de pago en un factor de n (que tiende a crecer sin límite) y se reduce la tasa de interés en el período, en un factor de \textstyle {1 \over n}, el total de unidades monetarias obtenidas está expresado por la siguiente ecuación:
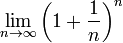
Las primeras referencias a la constante fueron publicadas en 1618 en la tabla en un apéndice de un trabajo sobre logaritmos de John Napier.2 No obstante, esta tabla no contenía el valor de la constante, sino que era simplemente una lista de logaritmos naturales calculados a partir de ésta. Se cree que la tabla fue escrita por William Oughtred.
El "descubrimiento" de la constante está acreditado a Jacob Bernoulli, quien estudió un problema particular del llamado interés compuesto. Si se invierte una Unidad Monetaria (que abreviaremos en lo sucesivo como UM) con un interés del 100% anual y se pagan los intereses una vez al año, se obtendrán 2 UM. Si se pagan los intereses 2 veces al año, dividiendo el interés entre 2, la cantidad obtenida es 1 UM multiplicado por 1,5 dos veces, es decir 1 UM x 1,502 = 2,25 UM. Si dividimos el año en 4 períodos (trimestres), al igual que la tasa de interés, se obtienen 1 UM x 1,254 = 2,4414... En caso de pagos mensuales el monto asciende a 1 UM x (1+\textstyle{1 \over 12})^{12} = 2,61303...UM. Por tanto, cada vez que se aumenta la cantidad de períodos de pago en un factor de n (que tiende a crecer sin límite) y se reduce la tasa de interés en el período, en un factor de \textstyle {1 \over n}, el total de unidades monetarias obtenidas está expresado por la siguiente ecuación:
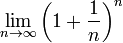
Bernoulli comprobó que esta expresión se aproxima al valor de 2,7182818...UM. De aquí proviene la definición que se da de e en finanzas, que expresa que este número es el límite de una inversión de 1 UM con una tasa de interés al 100% anual compuesto en forma continua. En forma más general, una inversión que se inicia con un capital C y una tasa de interés anual R, proporcionará Ce^R UM con interés compuesto.
El primer uso conocido de la constante, representado por la letra b, fue en una carta de Gottfried Leibniz a Christiaan Huygens en 1690 y 1691. Leonhard Euler comenzó a utilizar la letra e para identificar la constante en 1727, y el primer uso de e en una publicación fue en Mechanica, de Euler, publicado en 1736. Mientras que en los años subsiguientes algunos investigadores usaron la letra c, e fue la más común, y finalmente se convirtió en la terminología usual.
En 1873, Charles Hermite (1822-1905) logró demostrar que e es trascendente, a dicho logro llegó usando un polinomio, conseguido con ayuda de fracciones continuas, empleadas ,anteriormente, por Lambert. David Hilbert — también Karl Weierstrass y otros — propusieron, posteriomente, variantes y modificaciones de las primeras demostraciones.
El primer uso conocido de la constante, representado por la letra b, fue en una carta de Gottfried Leibniz a Christiaan Huygens en 1690 y 1691. Leonhard Euler comenzó a utilizar la letra e para identificar la constante en 1727, y el primer uso de e en una publicación fue en Mechanica, de Euler, publicado en 1736. Mientras que en los años subsiguientes algunos investigadores usaron la letra c, e fue la más común, y finalmente se convirtió en la terminología usual.
En 1873, Charles Hermite (1822-1905) logró demostrar que e es trascendente, a dicho logro llegó usando un polinomio, conseguido con ayuda de fracciones continuas, empleadas ,anteriormente, por Lambert. David Hilbert — también Karl Weierstrass y otros — propusieron, posteriomente, variantes y modificaciones de las primeras demostraciones.
HISTORIA DE LA LETRA GRIEGA PI
Letra griega pi. Símbolo adoptado en1706 por William Jones y popularizado porLeonhard Euler.
La notación con la letra griega π proviene de la inicial de las palabras de origen griego "περιφέρεια" (periferia) y "περίμετρον" de un círculo,1 notación que fue utilizada primero por William Oughtred (1574-1660), y propuesto su uso por el matemático galés William Jones2 (1675-1749), aunque fue el matemático Leonhard Euler, con su obra «Introducción al cálculo infinitesimal» de 1748, quien la popularizó. Fue conocida anteriormente como constante de Ludolph (en honor al matemático Ludolph van Ceulen) o como constante deArquímedes (que no se debe confundir con el número de Arquímedes).
La notación con la letra griega π proviene de la inicial de las palabras de origen griego "περιφέρεια" (periferia) y "περίμετρον" de un círculo,1 notación que fue utilizada primero por William Oughtred (1574-1660), y propuesto su uso por el matemático galés William Jones2 (1675-1749), aunque fue el matemático Leonhard Euler, con su obra «Introducción al cálculo infinitesimal» de 1748, quien la popularizó. Fue conocida anteriormente como constante de Ludolph (en honor al matemático Ludolph van Ceulen) o como constante deArquímedes (que no se debe confundir con el número de Arquímedes).
antiguo egipto
mesopotamia
Historia del número áureo
El
número áureo se encuentra como proporción en varias estelas de
Babilonia y Asiria de alrededor de 2000 a. C. Sin embargo, no existe
documentación histórica que indique que el número áureo fuera utilizado
conscientemente por dichos artistas en la elaboración de las estelas.
Cuando se mide una estructura compleja, es fácil obtener resultados
curiosos si se tienen muchas medidas disponibles.
tu blog esta chevere con la musica y eso que que esta dando vueltas.
ResponderEliminarEstuvo interesante el tema sobre el numero neperiano