Relaciones y Funciones
Definición matemática de Relación y de Función
En matemática, Relación es la correspondencia de un primer
conjunto, llamado Dominio, con un segundo conjunto, llamado Recorrido o Rango,
de manera que a cada elemento del Dominio le corresponde uno o más elementos
del Recorrido o Rango.
Por su parte, una Función es una relación a la cual se añade
la condición de que a cada valor del Dominio le corresponde uno y sólo un valor
del Recorrido.
De las definiciones anteriores podemos deducir que todas las
funciones son relaciones, pero no todas las relaciones son funciones.
También debemos agregar que toda ecuación es una Relación,
pero no toda ecuación es una Función.
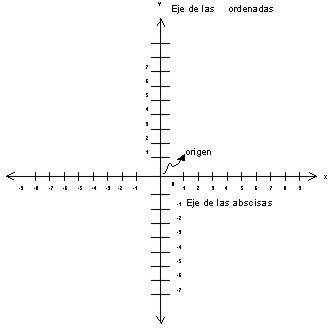
Todas las Relaciones pueden ser graficadas en el Plano
Cartesiano.
Dados dos conjuntos A y B una relación definida de A en B es
un conjunto de parejas ordenadas (par ordenado) que hacen verdadera una
proposición; dicho de otro modo, una relación es cualquier subconjunto del
producto cartesiano A x B
Ejemplos
Ejemplo 1.
Si A = {2, 3} y B =
{1, 4, 5}, encontrar tres relaciones definidas de A en B.
Solución
El producto cartesiano de A x B está conformado por las
siguientes parejas o pares ordenados:
A x B =
{(2, 1), (2, 4), (2, 5), (3, 1), (3, 4), (3, 5)}
Y cada uno de los siguientes conjuntos corresponde a
relaciones definidas de A en B:
R1
= {(2, 1), (3, 1)}
R2
= {(2, 4), (2, 5), (3, 4), (3, 5)}
R3
= {(2, 4), (3, 5)}
La relación R1 se puede definir como el conjunto de pares
cuyo segundo elemento es 1, esto es, R1 =
{(x, y) / y = 1}.
La relación R2 está formada por los pares cuyo primer
componente es menor que el segundo componente, R2 = {(x, y) / x < y}
Y la relación R3 está conformada por todos los pares que
cumplen con que el segundo componente es dos unidades mayor que el primer
componente, dicho de otro modo, R3 =
{(x, y) / y = x + 2}
Así, se puede continuar enumerando relaciones definidas a
partir de A x B. Como se puede ver, la regla que define la relación se puede
escribir mediante ecuaciones o desigualdades que relacionan los valores de x e
y. Estas reglas son un medio conveniente para ordenar en pares los elementos de
los dos conjuntos.
Dominio y rango de una relación
El dominio de una relación es el conjunto de preimágenes; es
decir, el conjunto formado por los elementos del conjunto de partida que están
relacionados. Al conjunto de imágenes, esto es, elementos del conjunto de
llegada que están relacionados, se le denomina recorrido o rango.
Ejemplo 2
Sea A = {1, 2, 3, 4}
y B = {4, 5, 6, 7, 8} y R la relación definida de A en B determinada por
la regla “y es el doble de x” o “y = 2x”, encontrar dominio y rango de la
relación.
Solución
El total de pares ordenados que podemos formar, o producto
cartesiano es:
A x B = {(1, 4), (1,
5), (1, 6), (1, 7), (1, 8), (2, 4), (2, 5), (2, 6), (2, 7), (2, 8), (3, 4), (3,
5), (3, 6), (3, 7), (3, 8), (4, 4), (4, 5), (4, 6), (4, 7), (4, 8)}
Pero los pares que pertenecen a la relación R (y = 2x) son
solo:
R =
{(2, 4), (3, 6), (4, 8)}
En esta relación vemos que: “4 es el doble de 2”; esto es,
“4 es la imagen de 2 bajo R”, dicho de otro modo, “2 es preimagen de 4”.
Así, el dominio y rango son:
D = {2, 3, 4}
Rg = {4, 6, 8}
Según lo que vemos, ¿Qué relación hay entre el Dominio y el
conjunto de partida?
En el Dominio falta el elemento 1 del conjunto de partida,
por lo tanto el Dominio es un subconjunto de A.
Otra pregunta: ¿Todo elemento del conjunto de llegada es
elemento del rango?
La respuesta es no, pues en el rango faltan el 5 y el 7.
Representación gráfica de las relaciones
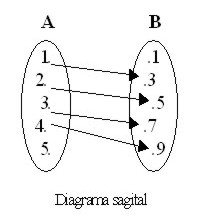
Los pares ordenados se pueden representar gráficamente por medio de diagramas sagitales o por medio de puntos en el plano cartesiano. Veamos el siguiente ejemplo.Ejemplo3
Si A = {1, 2, 3, 4, 5} y B = {1, 3, 5, 7, 9} y R la relación definida por la regla
R = {(x, y) / y = 2x + 1}, graficar R.
Solución
Los pares ordenados que pertenecen a la relación (que cumplen con y = 2x + 1) son:
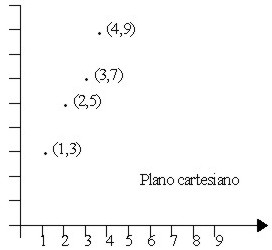
R = {(1, 3), (2, 5), (3, 7), (4, 9)}
Y la gráfica correspondiente es la siguiente:

No hay comentarios:
Publicar un comentario